1. 有一个矩形的花园,面积是2400平方米,且绕着花园走一圈是220米,问该花园较长的一条边长度为多少?
A.30米
B.40米
C.60米
D.80米
2. 如图ABCD是一个梯形,E是AD的中点,直线CE把梯形分成甲、乙两部分,其面积之比是15∶7。问上底AB与下底CD的长度之比是:
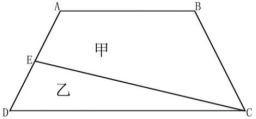

A.5∶7
B.6∶7
C.4∶7
D.3∶7
3. 某城市准备在公园里建一个矩形的花园,长比宽多40米,同时在花园周围建一条等宽的环路。路的外周长为280米,路的面积为1300平方米,则路的宽度为多少米?
A.3
B.4
C.5
D.6
4. 一个矩形的长、宽和为10cm,如果长增加2cm、宽不变,矩形面积增加6cm²。原来的矩形面积是()cm²
A.25
B.24
C.21
D.16
5. 赵家和王家都使用90米的篱笆围成了长方形的菜园,已知王家的长方形菜园的长边比赵家短5米,但是菜园面积却比赵家大50平方米,则王家的长方形菜园面积为:
A.550平方米
B.500平方米
C.450平方米
D.400平方米
翻页查看解析答案哦~

2022云南事业单位备考群
加群了解更多考试信息,获取更多备考资料
1.【答案】D
【解析】
第一步,本题考查几何问题,属于平面几何类。
第二步,由题意可设边长为a,b,则a+b=110,ab=2400,解得b=80(米)。
因此,选择D选项。
2.【答案】C
【解析】
解法一:
第一步,本题考查几何问题,属于平面几何类。


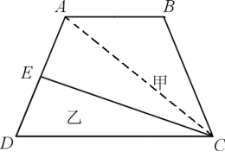


因此,选择C选项。
解法二:
第一步,本题考查几何问题,属于平面几何类。
第二步,由E为AD中点知,梯形的高等于三角形高的二倍,设三角形高为h,梯形高为2h。梯形ABCD的面积为:(AB+CD)×2h÷2,三角形ECD的面积为:CD×h÷2,则梯形ABCD的面积与三角形ECD的面积的比值为2(AB+CD)∶CD=(15+7)∶7,化简得AB∶CD=4∶7。
因此,选择C选项。
3.【答案】C
【解析】
第一步,本题考查几何问题,属于平面几何类。
第二步,设长方形的长为x米,宽为x-40米,设增设环路的宽为y米,则增建环路之后的长方形的长为x+2y米,宽为x-40+2y米。由题目已知条件可列方程:2×(x+2y+x-40+2y)=280①,(x+2y)(x-40+2y)-x(x-40)=1300②,由方程①优先解得x+2y=90,代入方程②解得x=80(米),y=5(米)。
因此,选择C选项。
4.【答案】C
【解析】
第一步,本题考查几何问题,属于平面几何类。
第二步,设原来的矩形的长为x厘米,则宽为10-x厘米,长增加2cm后为x+2厘米,可列式(x+2)(10-x)=x(10-x)+6,解得x=7(厘米),则原来的矩形面积是7×3=21cm²。
因此,选择C选项。
5.【答案】B
【解析】
第一步,本题考查几何问题,属于平面几何类。
第二步,由长方形可知,两家菜园的长宽之和均为90÷2=45(米)。设王家菜园长为x米,宽为(45-x)米;根据王家长边比赵家短5米,可知赵家长为(x+5)米,宽为(40-x)米。
第三步,由王家面积比张家大50,可得x(45-x)-(x+5)(40-x)=50,解得x=25。故王家菜园面积为25×20=500(平方米)。
因此,选择B选项。











